Что называется дугой окружности. Условие перпендикулярности прямых
Окружность
- это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность - это линия
на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Условие параллельности прямых
Если дуга содержит не более 60 градусов, относительная погрешность этой формулы составляет менее 5%. Следовательно, все вписанные углы, основанные на одной и той же дуге, равны. Поскольку центральный угол содержит то же количество градусов, что и его дуга, то любой вписанный угол измеряется половиной дуги, на которой основана. Это свойство можно рассматривать как частный случай на рис.
Многие объекты, которые мы встречаем в нашей повседневной жизни, «круглые» по форме. Монета, браслеты, колпачки для бутылок, Земля, колеса и т.д. в непрофессиональных условиях круглую форму часто называют кружком. Закрытая плоская фигура, образованная множеством всех тех точек, которые равноудалены от неподвижной точки в одной плоскости, называется кругом. Фиксированная точка называется центром круга, а постоянное расстояние между любой точкой на окружности и ее центром называется радиусом. Окружность круга может быть определена как расстояние вокруг него.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой . Хорда, проходящая через центр окружности, представляет собой диаметр . Диаметр окружности равен ее удвоенному радиусу: D = 2R .

Другими словами, а можно описать как локус точки, движущейся в плоскости, таким образом, чтобы ее расстояние от неподвижной точки всегда было постоянным. Круг любого конкретного радиуса можно легко проследить с помощью компаса. Заостренная ножка компаса помещается на бумаге, а подвижная ножка вращается, как показано.
Прослеживаемый рисунок дает нам круг. На рисунке, показанном выше, различные точки отмечены лежащими либо снаружи, либо внутри круга, либо на круге. Исходя из этого, любая точка может быть определена как. Внешняя точка: точки, лежащие в плоскости круга, такие, что его расстояние от центра больше, чем радиус круга, являются внешними точками. Внутренние точки: точка, лежащая в плоскости круга, такая, что ее расстояние от ее центра меньше радиуса круга, называется внутренней точкой. Точка на окружности круга: точки, лежащие в плоскости круга, так что его расстояние от центра равно радиусу окружности. Простыми словами, множество точек, лежащих на окружности, являются точками на окружности круга. Теперь, когда мы знаем о точке и ее относительном положении относительно круга, обсудим линию и ее относительное положение по кругу.
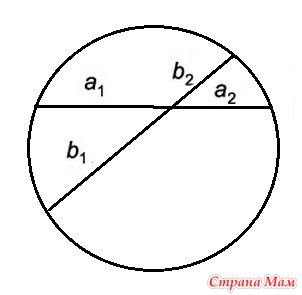
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
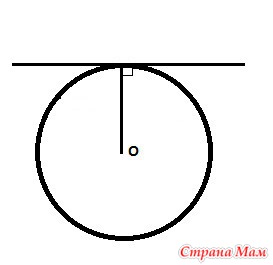
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Учитывая линию и круг, она может касаться круга или не касаться, как показано ниже. Хорда, проходящая через центр круга, называется диаметром круга и является самой большой хордой круга. Линия, касающаяся круга в одной точке, называется касательной к кругу.
На последнем рисунке линия нигде не касается круга, поэтому она называется непересекающейся линией. Теперь обсудим круговую область, которая отрезана от остальной части круга секущей или аккордом. Часть окружности круга называется дугой. Дуга представляет собой сплошную часть круга.
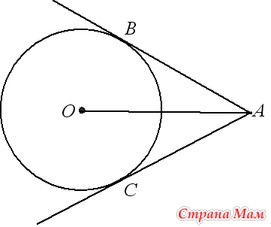
Отрезки касательных к окружности, проведенные из одной точки, равны : AB = AC, центр окружности лежит на биссектрисе угла BAC.
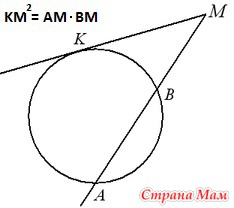
Квадрат касательной равен произведению секущей на ее внешнюю часть
Часть круга, ограниченная хордой и дугой, называется сегментом окружности. Приведенная ниже фигура изображает основной и второстепенный сегменты круга. Можно ли увидеть две специальные поверхности: круглую и круглую. Сначала начнем с дуги окружности, которая нам нужна для круговых и круговых секций.
Под одним мы понимаем часть круга. Подобно тому, как круговая дуга является частью круга, круговое сечение является частью круговой поверхности. Это также называют районным сектором. Вы можете представить себе это как кусочки торта. Как известно, площадь круга может быть рассчитана с помощью этой формулы.
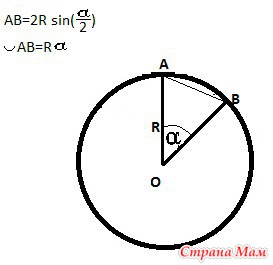
Центральный угол - это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вы хотите испечь пиццу со своей девушкой. Поскольку вы знаете радиус пиццы, вы также можете рассчитать площадь в квартал. Круговой участок также является частичной областью круговой области. Круг - это расстояние между двумя точками круга. Теперь центр круга должен определяться геометрически.
Для этого мы выбираем по крайней мере 3 случайных точки на линии круга, которые должны быть конечными точками 2 круглых аккордов. Чтобы геометрически определить центр круга, мы строим растягивающие симметрии двух круговых аккордов. Две растянутые симметрии пересекаются в точке, центре круга.
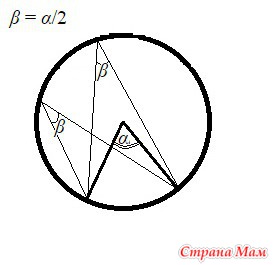
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Чтобы иметь возможность построить вторую симметрию растяжения, соединяем точки В и С вместе. Затем мы строим растянутую симметрию из разработанного таким образом кругового сегмента. Две растянутые симметрии пересекаются друг с другом в центре круга. Для целей управления или для повышения точности ручного дизайна можно было бы, конечно, также построить любое количество других симметрий растяжения.
Центрировать центр круга. Выберите 3 точки на круге и соедините их. Постройте симметрию растяжения по меньшей мере из двух этих маршрутов. Точка, в которой встречаются две симметрии растяжения, является центром круга. Протяжная симметрия - австрийская - скажите это по-немецки!
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
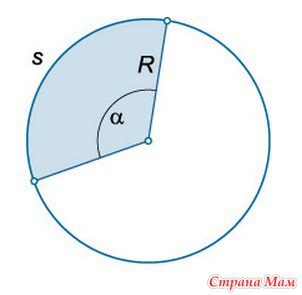
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = П R 2 а /360°.
Подключите точки пересечения дуг. Чтобы нарисовать «растягивающуюся симметрию», нужно определить центр полученной прямой линии, а затем провести прямую линию от этой точки под углом 90 °. Математическая отрасль, изучающая свойства, формы и размеры фигур и геометрических тел.
Знак, который оставляет карандаш на бумаге, настолько мал, что ему не хватает размеров. Часть линии ограничена двумя несоответствующими точками. Это та линия, которая не имеет прямых частей. Кривая часть ограничена двумя несоответствующими точками. Расширение ограничено точками, линиями и поверхностями.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Прямая
Плоскость
Общее уравнение прямой. Нормальный вектор.
Уравнение прямой с угловым коэффициентом.
Уравнение прямой в отрезках на осях. Уравнение прямой, проходящей
Это все, что занимает место в пространстве и имеет длину, ширину и высоту. Дополнительные углы: дополнительные углы - это те, чьи меры составляют до 180 °. Дополнительные углы: дополнительными углами являются углы, чьи меры суммарно 90 ° Угол конъюгата: он называется двумя углами, размеры которых составляют 360 °.
Теория конгруэнции. Гомологичные стороны. Это те, у которых смежные углы равны. Это те, которые имеют одинаковую форму и размер. Теорема о таком: когда в треугольнике нарисована линия, параллельная одной из сторон, образующийся треугольник аналогичен первому.
через две различные точки. Параметрическое уравнение прямой.
Условие параллельности прямых. Условие перпендикулярности прямых.
Расстояние между двумя точками. Расстояние от точки до прямой.
Расстояние между параллельными прямыми. Угол между прямыми.
Общее уравнение прямой:
Ах + Ву + С = 0 ,
Если два треугольника конгруэнтны, то: Теорема Пифагора: во всех правильных треугольниках квадрат гипотенузы равен сумме квадратов ног. Их коллеги одинаковы. Четырехугольник: любой многоугольник из четырех сторон. Их гомологичные углы одинаковы. Диагональ: это отрезок линии, соединяющий две вершины несмежного четырехугольника.
Сумма внутренних углов четырехугольника равна 360 °
Это плоская закрытая фигура, ограниченная сегментами прямой. Они классифицируются в соответствии с измерением их сторон или углов. Регулярно: они имеют все свои стороны одинаково. Выпуклый: внутренние углы меньше 180 °. Нерегулярные: у них есть мера их разных сторон. Вогнутый: один из его внутренних углов больше 180 °.
где А и В не равны нулю одновременно.
Коэффициенты А и В являются координатами нормального вектора прямой (т.е. вектора, перпендикулярного прямой). При А = 0 прямая параллельна оси ОХ , при В = 0 прямая параллельна оси ОY .
При В 0 получаем уравнение прямой с угловым коэффициентом :
Это точка, в которой согласны две стороны. Это тот, который сформирован с двумя смежными сторонами многоугольника. Тот, который образуется между продолжением одной стороны и ее смежной стороны. Это сегмент линии, который связывает две несмежные вершины.
Это множество точек, которые являются эквидистами из неподвижной точки, называемой центром, и ее длина представляет периметр круга. Он определяется как поверхность, ограниченная окружностью. Это имя сегмента линии, соединенного центром и любой точкой на окружности.
Это называется сегментом линии, который соединяет 2 точки окружности без прохождения через центр. Это, таким образом, называется самой большой веревкой, которая соединяет две противоположные точки окружности и проходит через центр. Эта прямая, проходящая через 2 точки окружности.
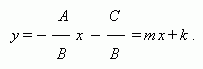
Уравнение прямой, проходящей через точку (х 0 , у 0 ) и не параллельной оси OY , имеет вид:
у – у 0 = m (x – х 0) ,
где m – угловой коэффициент , равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .
Это перпендикуляр, оттянутый от точки по окружности до середины струны. Это сумма сторон многоугольника. Это область плоскости, ограниченная фигурой в двух измерениях. Это длина сегмента, который соединяет центр многоугольника и середину одной из сторон.
Или Евклида - это часть математики, которая изучает цифры, которые не имеют объема. Плоская геометрия также называется евклидовой, так как ее имя представляет собой дань геометрии евклидов Александрии, считающихся «отцом геометрии». Некоторые понятия имеют большое значение для понимания плоской геометрии, а именно.
При А 0, В 0 и С 0 получаем уравнение прямой в отрезках на осях :
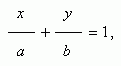
где a = – C / A , b = – C / B . Эта прямая проходит через точки (a , 0) и (0, b ), т.е. отсекает на осях координат отрезки длиной a и b .
Уравнение прямой, проходящей через две различные точки (х 1 , у 1) и (х 2 , у 2):
Безразмерная концепция, поскольку она не имеет размерности. Точки определяют местоположение и обозначаются прописными буквами. Линия, представленная строчной буквой, является неограниченной одномерной линией и может быть представлена в трех положениях.
В зависимости от положения линий, когда они пересекаются, т.е. имеют общую точку, они называются конкурирующими линиями. С другой стороны, те, у которых нет общих точек, классифицируются как параллельные линии. В отличие от прямой линии, сегмент линии ограничен, так как он соответствует части между двумя различными точками.
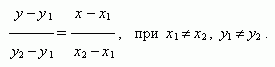
Параметрическое уравнение прямой , проходящей через точку (х 0 , у 0 ) и параллельной направляющему вектору прямой (a , b ) :
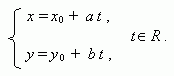
Условие параллельности прямых:
Полукруг ограничен только в одном смысле, поскольку он имеет начало и не имеет конца. Соответствует плоской двумерной поверхности, то есть имеет два размера: длину и ширину. На этой поверхности образуются геометрические фигуры. Углы образованы объединением двух прямых сегментов, от общей точки, называемой вершиной угла.
Острый угол. . Площадь геометрической фигуры выражает размер поверхности. Таким образом, чем больше поверхность фигуры, тем больше ее площадь. Периметр представляет собой сумму всех сторон геометрической фигуры. Многоугольник трех сторон, треугольник представляет собой плоскую геометрическую фигуру, образованную тремя прямыми сегментами.
1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AE – BD = 0 ,
2) для прямых у = m x+ k и у = p x+ q : m = p .
Условие перпендикулярности прямых:
1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AD + BE = 0 ,
2) для прямых у = m x+ k и у = p x+ q : m p = – 1 .R > 0 называется радиусом окружности .
Согласно форме треугольников, они подразделяются на. Равносторонний треугольник: имеет все стороны и внутренние углы равные, равнобедренный треугольник: имеет две стороны и два конгруэнтных внутренних угла, треугольник скальена: имеет все стороны и разные внутренние углы. Что касается углов, которые образуют треугольники, они классифицируются следующим образом.
Прямоугольный треугольник: имеет внутренний угол 90 °, треугольник обтаскания: имеет два острых угла внутреннего, т.е. менее 90 °, и внутренний тупой угол, более 90 °, треугольный угол: имеет три внутренних угла меньше 90 °. Узнайте больше о треугольниках, прочитав статьи.
Уравнение окружности радиуса R с центром в точке О (х 0 , у 0) имеет вид:
(х – х 0) 2 + (у – у 0) 2 = R 2 .
Если центр окружности совпадает с началом координат , то уравнение окружности упрощается:
х 2 + у 2 = R 2 .
Многоугольник из четырех равных сторон, квадрат или четырехугольник - плоская геометрическая фигура, которая имеет четыре угла конгруэнтных: прямые. Узнайте больше об этом, прочитав статьи. Плоская геометрическая фигура, отмеченная двумя параллельными сторонами в вертикальном направлении и двумя другими параллелями, горизонтально. Таким образом, все стороны прямоугольника образуют прямые углы.
Посмотрите статьи на прямоугольник. Плоская геометрическая фигура, характеризующаяся множеством всех точек плоскости. Радиус круга соответствует мере расстояния между центром фигуры и ее концом. Мера - это объект, используемый для рисования кругов и кругов.
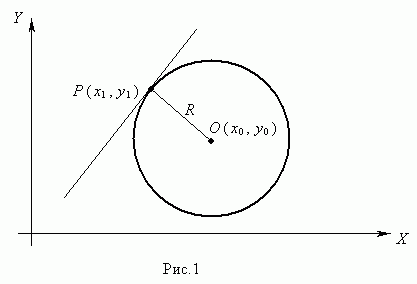
Пусть Р (х 1 , у 1) – точка окружности (рис.1), тогда уравнение касательной к окружности в данной точке имеет вид:
(х 1 – х 0) (х – х 0) + (у 1 – у 0) (у – у 0) = R 2 .
Условие касания прямой y = m x + k и окружности х 2 + у 2 = R 2:
k 2 / (1 + m 2) = R 2 .